Using Web Map Service Data for Visualization and Analysis in Geospatial Applications
By Alan Hwang, MathWorks and Kelly Luetkemeyer, MathWorks
Geographic data sets and base maps are available on the Internet in ever-increasing numbers, but finding the right data for your application can be difficult. You may need to sift through hundreds of databases or download and combine many files to get the necessary coverage. You may find a Web site with appropriate data only to learn that this data is not available to the public. The solution to many of these problems is Web Map Service (WMS), a protocol developed by the Open Geospatial Consortium for serving geographic data, rendered as a pictorial map, over the Internet.
Many government organizations, including the National Aeronautical and Space Administration (NASA), the National Oceanic and Atmospheric Administration (NOAA), the European Space Agency (ESA), and the United States Geological Survey (USGS), use this protocol to provide a vast array of data to the public. Applications for available geographic data layers include atmospheric and ocean studies, oil and gas exploration, natural resource management, financial analysis, and urban planning.
This article demonstrates how you can use Mapping Toolbox™ functions to find geospatial raster data, render WMS maps, and visualize and analyze retrieved data. The following topics are covered:
Accessing Data from a WMS Server
You can find and display an appropriate WMS layer with just a few lines of code. For our sample search, we will find the “Blue Marble Next Generation, Global MODIS derived image” or bmng layer from a server located at NASA’s Jet Propulsion Laboratory (JPL). Using the wmsfind function in Mapping Toolbox, we search the installed database for layers containing a match for the query string “blue marble.” The result is a WMSLayer array that contains multiple layers from multiple servers.
layers = wmsfind('blue marble');
jplLayers = layers.refine(...
'jpl','SearchField','serverurl');
bmng = jplLayers.refine('bmng');
We use the wmsread function to retrieve the data, rendered as a RGB image. The geoshow function is used to project and display the imagery in a map frame (Figure 1).
[backdrop, R] = wmsread(bmng); figure, axesm robinson; geoshow(backdrop, R);
In geospatial applications, it is often necessary to model time-varying data sets. The WMS protocol supports the retrieval of data for different time periods. This example shows how to use WMS functionality to uncover longterm trends in the distribution of sea ice. Visualizing trends in sea ice measurements helps climatologists understand the effects of climate change on Arctic marine ecology.
First, we download polar sea ice measurements. The installed database contains many ice-related data layers. We refine the search to include animated data, and narrow the results to a layer located at the NASA Goddard Space Flight Center. The data set provides measurements of sea ice from 1979 to 2004. Once the layer has been identified, we download the data by nesting the wmsread function in a for-loop. This process creates a 4D matrix of color images representing the mean sea ice for the month of September from 1979 to 2004.
By combining the ice data with the Blue Marble image, we can visualize the distribution of sea ice at the Northern polar ice cap with a reference backdrop. With Mapping Toolbox we align the data sets for quantitative comparison and create a Lambert Azimuthal Equal-Area projection for latitudes 500 to 900. Sea ice in 1980, 1999, and 2004 is displayed; the results show how the sea-ice area has contracted over 25 years (Figure 2).
The image is informative, but it does not tell us how much the sea ice has receded since 1980. To obtain this information, we use the Mapping Toolbox areamat function to calculate the surface area of sea ice.
We plot the result and find that mean sea ice levels in 2001 to 2004 are approximately 15% lower than 1980s levels (Figure 3). A simple linear fit demonstrates this downward trend. To perform a more comprehensive analysis, we could gather more data and create a model that takes seasonal effects into account.
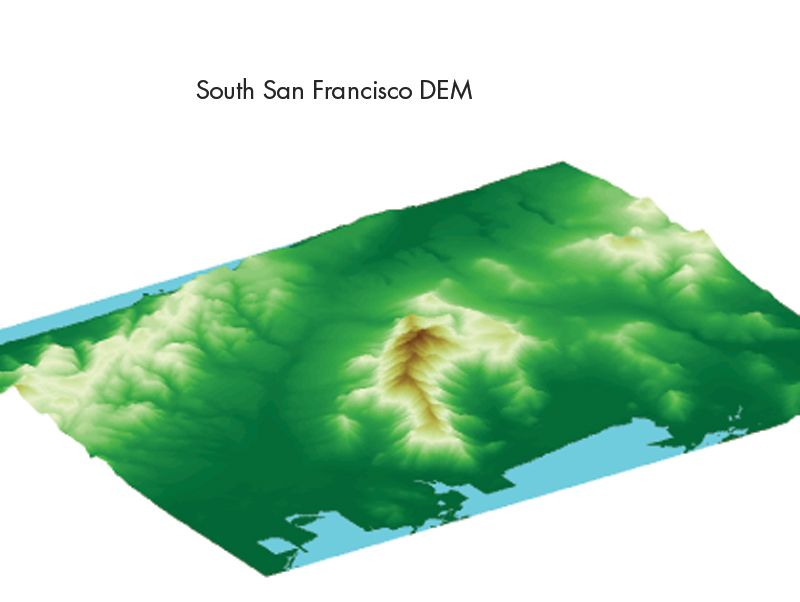
An orthophoto is an aerial photograph that has taken elevation, lens distortion, and camera angle into account so that the scale is uniform and true distances can be measured. In this example, we drape an orthophoto onto a 3D surface rendering of the National Elevation Dataset (NED), a digital elevation model (DEM) that provides elevation data in raster format for the United States and is accessible via WMS. Using Mapping Toolbox, we retrieve the NED, with customized latitude and longitude and image height and width, and render the map (Figure 4).
We search the installed database for layers from the Microsoft® TerraServer, which hosts many orthophotos and topographic maps from the USGS. Once we find an appropriate layer, we use the same parameters to retrieve the map from the WMS server that we used to retrieve the NED. The orthophoto is then returned with appropriate latitude and longitude extents and resolution. We use the Image Processing Toolbox™ imshow function to display the image (Figure 5).
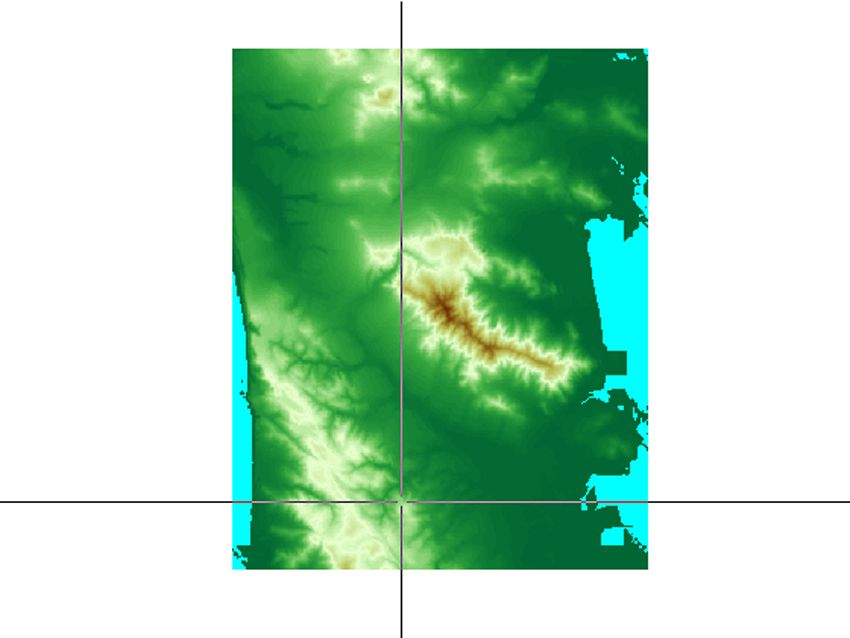
We combine the orthophoto and DEM by setting the color data of the DEM plot as the aerial image. Since the WMS server has already resized the image with limits and orientation that coincide with the DEM data, the surfaces align and display correctly (Figure 6). With Mapping Toolbox terrain analysis functionality, we can further explore the DEM data. For example, we can calculate a viewshed, an analysis that reveals which portions of a landscape are seen by an observer from a specific vantage point. The viewshed function assigns a value of 1 to visible areas and a value of 0 to all other areas. In Figure 7, we select a point in the valley from which to calculate the viewshed.
We compare this viewshed to that obtained from the highest point on the mountain range. The resulting data is visualized in the same manner used to drape the orthophoto over the elevation model.This visualization enables a side-by-side comparison, where non-visible areas are darkened with a shadow (Figure 8). Positioning an observer at the highest point considerably improves visibility of the area.
Viewshed calculations are important in many applications. For example, you can use the viewshed function to place cell phone towers in locations that have extensive coverage. You can then use WMS functionality to download population density, correlate the viewshed with the population density, and optimize the number of subscribers who will have service.
Data obtained via WMS can be combined with other data sets to yield further insight. In this example, we combine two WMS data sets: earthquake frequency and population density. The result indicates which areas may be at more risk in the event of seismic activity.
There are two earthquake data layers. The first contains a mapping of tectonic plates. The second contains the frequency of earthquakes over a 15-year period. Figure 9 displays the tectonic plates and the seismic activity (represented by earthquake frequencies along plate borders). In the second layer, yellow indicates 1 to 2 earthquakes; orange, approximately 10 earthquakes; and red, 50 to 200 earthquakes.
We combine the earthquake frequency data with the second data set, estimated population density in 1995. The population density is accompanied by a legend, which we display with the layer in Figure 10.
Before combining data sets, we must complete two steps. First, we convert the red, green, and blue channels of the WMS data layers to intensity. In this example, the data was returned from the WMS server as a color image with a legend that indicates the population density. The rgb2ind function enables us to convert an RGB image into an indexed image based on a color map. We can modify the resulting indices to match the population scale of the legend.
Second, we normalize the maximum value of each data set to 1 so that we can apply an appropriate weighting when fusing the images. The population data ranges from 1 to 10,000 people per square kilometer, while the earthquake data ranges from 1 to 200 earthquakes in 15 years. One approach to fusing the data sets is to apply a simple weighted average in locations where both data sets exist (Figure 11).
RiskMetric(lat,lon)= α×EarthquakeFreq(lat,lon) +β×PopulationDensity(lat,lon)
We can tune the risk calculation by changing the coefficients α and β to weight either earthquake frequency or population density. This is the beginning of a more complicated analysis for earthquake zones. We can include other data layers, such as how well structures are reinforced, the inhabitants’ earthquake readiness, and even time of day.
RiskMetric(lat,lon)= F(EarthquakeFreq(lat,lon), PopulationDensity(lat,lon), EarthquakeFunding(lat,lon),…)
When multiple data sets are combined, the risk analysis becomes a function of several variables and can more accurately estimate the consequences of seismic activity, such as how many people may be hurt or the amount of structural damage that the earthquake will cause.
Looking Ahead
As more organizations share their data over the Internet, the task of searching, sorting, and retrieving the appropriate data becomes more challenging. Tools that help find and visualize relevant data layers enable researchers, engineers, and scientists to quickly analyze and develop solutions to problems. Using Mapping Toolbox, we have demonstrated three examples of how WMS capabilities support this process by providing data for analysis, supplementing visualizations, and producing new insight by fusing multiple data sets.
WMS Support in Mapping Toolbox
Mapping Toolbox provides functions, tools, and utilities for analyzing geographic data and creating map displays. The new WMS features greatly expand the amount of geospatial data that you can access, and simplifies the process of finding and retrieving that data. Mapping Toolbox includes a prequalified database of WMS servers. You can search the database by keyword, server URL, geographic coordinates, or other terms and download the data layers best suited to your application.
Published 2010 - 91814v00