median
Median value of array
Syntax
Description
M = median( returns
the median value of A)A.
If
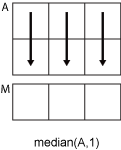
Ais a vector, thenmedian(A)returns the median value ofA.If
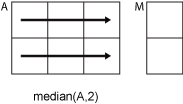
Ais a nonempty matrix, thenmedian(A)treats the columns ofAas vectors and returns a row vector of median values.If
Ais an empty 0-by-0 matrix,median(A)returnsNaN.If
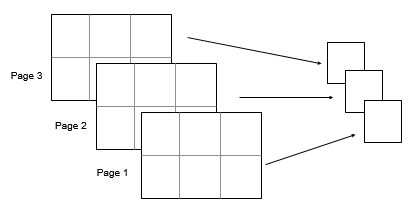
Ais a multidimensional array, thenmedian(A)treats the values along the first array dimension whose size is greater than1as vectors. The size ofMin this dimension becomes1, while the sizes of all other dimensions remain the same as inA.If
Ais a table or timetable, thenmedian(A)returns a one-row table containing the median of each variable. (since R2023a)
median returns natively in the class of A, such that
class(M) = class(A).
M = median(___, specifies
whether to include or omit missing values in missingflag)A for any of the
previous syntaxes. For example, median(A,"omitmissing") ignores
all missing values when computing the median. By default,
median includes missing values.
Examples
Input Arguments
Algorithms
For ordinal categorical arrays, MATLAB® interprets the median of an even number of elements as follows:
| If the number of categories between the middle two values is ... | Then the median is ... |
|---|---|
| zero (values are from consecutive categories) | larger of the two middle values |
| an odd number | value from category occurring midway between the two middle values |
| an even number | value from larger of the two categories occurring midway between the two middle values |
References
[1] “Weighted median.” In Wikipedia, May 21 2023. https://en.wikipedia.org/wiki/Weighted_median.