FMCW Waveforms
Benefits of Using FMCW Waveform
Radar systems that use frequency-modulated, continuous-wave (FMCW) waveforms are typically smaller and less expensive to manufacture than pulsed radar systems. FMCW waveforms can estimate the target range effectively, whereas the simplest continuous-wave waveforms cannot.
FMCW waveforms are common in automotive radar systems and ground-penetrating radar systems.
How to Create FMCW Waveforms
To create an FMCW waveform, use phased.FMCWWaveform. You
can customize certain characteristics of the waveform, including:
Sample rate.
Period and bandwidth of the FM sweep. These quantities can cycle through multiple values during your simulation.
Tip
To find targets up to a given maximum range,
r, you can typically use a sweep period of approximately5*range2time(r)or6*range2time(r). To achieve a range resolution ofdelta_r, use a bandwidth of at leastrange2bw(delta_r).Sweep shape. This shape can be sawtooth (up or down) or triangular.
Tip
For moving targets, you can use a triangular sweep to resolve ambiguity between range and Doppler.
phased.FMCWWaveform assumes that all frequency
modulations are linear. For triangular sweeps, the slope of the down
sweep is the opposite of the slope of the up sweep.
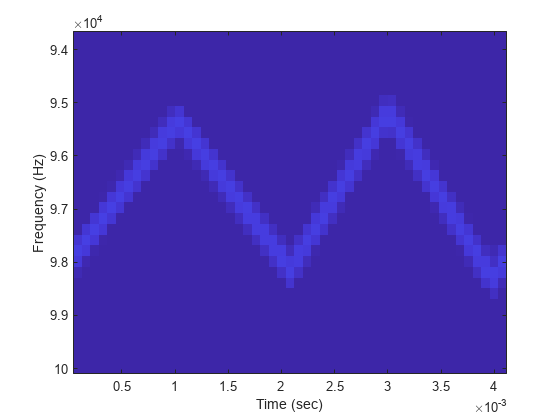
Double Triangular Sweep
This example shows how to sample an FMCW waveform with a double triangular sweep in which the two sweeps have different slopes. Then, the example plots a spectrogram.
Create an FMCW waveform object for which the SweepTime and SweepBandwidth properties are vectors of length two. For each period, the waveform alternates between the pairs of corresponding sweep time and bandwidth values.
st = [1e-3 1.1e-3]; bw = [1e5 9e4]; waveform = phased.FMCWWaveform('SweepTime',st,... 'SweepBandwidth',bw,'SweepDirection','Triangle',... 'SweepInterval','Symmetric','SampleRate',2e5,... 'NumSweeps',4);
Compute samples from four sweeps (two periods). In a triangular sweep, each period consists of an up sweep and down sweep.
x = waveform();
Plot the spectrogram.
[S,F,T] = spectrogram(x,32,16,32,waveform.SampleRate); image(T,fftshift(F),fftshift(mag2db(abs(S)))) xlabel('Time (sec)') ylabel('Frequency (Hz)')