pburg
Autoregressive power spectral density estimate — Burg’s method
Syntax
Description
pxx = pburg(x,order)pxx,
of a discrete-time signal, x, found using Burg’s
method. When x is a vector, it is treated as
a single channel. When x is a matrix, the PSD
is computed independently for each column and stored in the corresponding
column of pxx. pxx is the
distribution of power per unit frequency. The frequency is expressed
in units of rad/sample. order is the order of
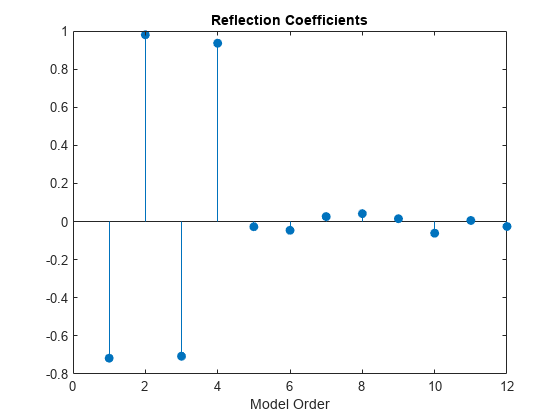
the autoregressive (AR) model used to produce the PSD estimate.
pxx = pburg(x,order,nfft)nfft points
in the discrete Fourier transform (DFT). For real x, pxx has
length (nfft/2+1) if nfft is
even, and (nfft+1)/2 if nfft is
odd. For complex–valued x, pxx always
has length nfft. If you omit nfft,
or specify it as empty, then pburg uses a default
DFT length of 256.
[
returns a frequency vector, pxx,f] = pburg(___,fs)f, in cycles per unit time. The sampling
frequency, fs, is the number of samples per unit time. If the unit of time
is seconds, then f is in cycles/second (Hz). For real-valued signals,
f spans the interval [0,fs/2] when
nfft is even and [0,fs/2) when
nfft is odd. For complex-valued signals, f spans the
interval [0,fs). fs must be the fourth input to
pburg. To input a sample rate and still use the default values of
the preceding optional arguments, specify these arguments as empty,
[].
[
returns the two-sided AR PSD estimates at the frequencies specified in the vector,
pxx,f] = pburg(x,order,f,fs)f. The vector f must contain at least two elements,
because otherwise the function interprets it as nfft. The frequencies in
f are in cycles per unit time. The sampling frequency,
fs, is the number of samples per unit time. If the unit of time is
seconds, then f is in cycles/second (Hz).
[___, returns
the pxxc] = pburg(___,'ConfidenceLevel',probability)probability × 100%
confidence intervals for the PSD estimate in pxxc.
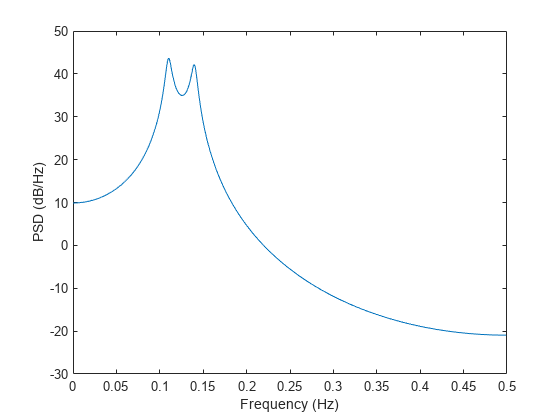
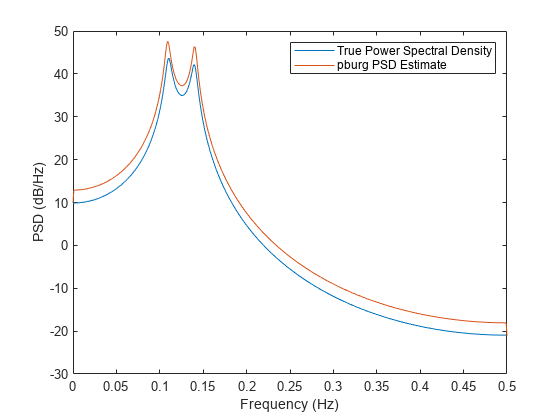
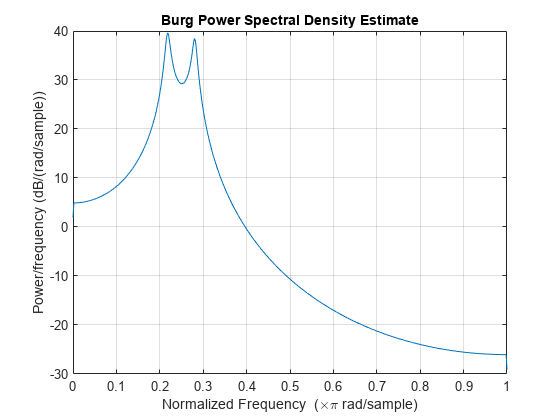
pburg(___) with no output arguments
plots the AR PSD estimate in dB per unit frequency in the current
figure window.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced before R2006a